Aufgabe 1
Die Punkte A(2|2|3), B(2|2|6) und C(2|5|3) bilden ein Dreieck.
- Ist das Dreieck gleichschenklig?
- Ist das Dreieck rechtwinklig?
- Bestimmen Sie den Flächeninhalt des Dreiecks.
Lösungen
Ergebnis: Die Seiten AB und AC haben die gleiche Länge, folglich ist das Dreieck ABC gleichschenklig.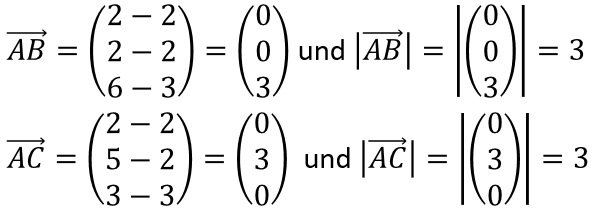
-
Wir haben zu prüfen, ob das Skalarprodukt
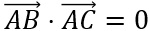ist.
Es folgt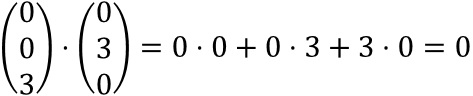
Ergebnis: Das Dreieck ist bei A rechtwinklig.
Ergebnis: Die Fläche des Dreiecks beträgt 4,5 LE2.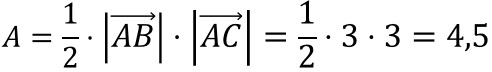
Aufgabe 2
Die Punkte A(3|1|4), B(-1|1|7) und C(6|x|8) bilden ein Dreieck.
Bestimmen Sie x so, dass das Dreieck mit
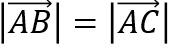gleichschenklig ist.
Lösung
Die Seiten AB und AC sollen gleich lang sein. Daher bestimmen wir zunächst die jeweiligen Vektoren und deren Länge:
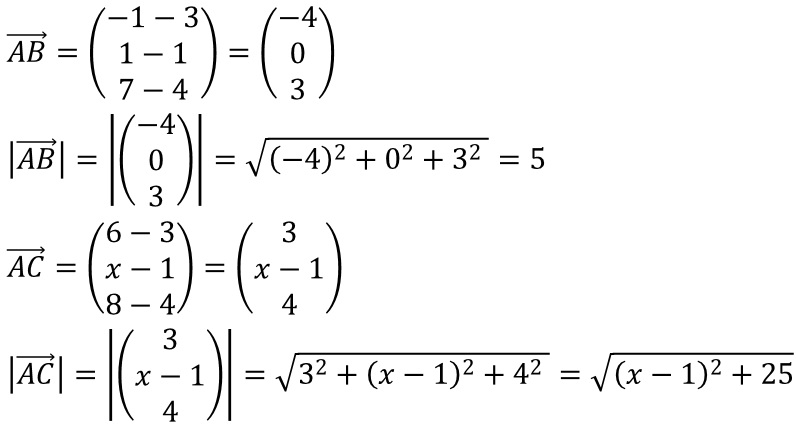
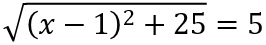| quadrieren(x-1)2+25=25 |-25
(x-1)2=0
Nun erkennt man sofort mit x=1 die Lösung.
Ergebnis: Der Punkt C(6|1|8) macht die Punkte A, B und C zu einem gleichschenkligen Dreieck.
Pflichtteil 2015 - Aufgabe 6
Gegeben sind die drei Punkte A(4|0|4), B(0|4|4), C(6|6|2).
- a) Zeigen Sie, dass das Dreieck ABC gleichschenklig ist.
- b) Bestimmen Sie die Koordinaten eines Punktes, der das Dreieck ABC zu einem Parallelogramm ergänzt.
Veranschaulichen Sie durch eine Skizze, wie viele solcher Punkte es gibt.(5 VP)
Lösung
a) Behauptung: Das Dreieck ABC ist gleichschenklig
Es gilt
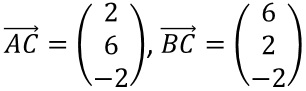also
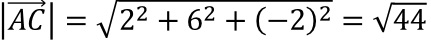und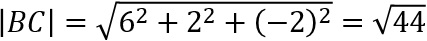 
. Folglich ist
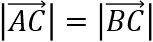und das Dreieck ABC wie behauptet gleichschenklig.b) Parallelogramm
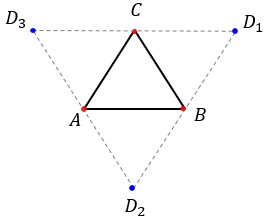
Wie die nebenstehende Skizze zeigt, gibt es drei Punkte, D1, D2 und D3, durch die das Dreieck zu einem Parallelogramm ergänzt werden kann.
Mit der Gleichung
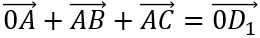lässt sich z.B. D1 bestimmen und es gilt:
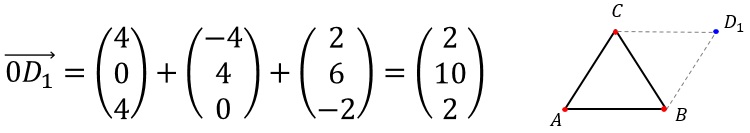
Analog erhält man die beiden anderen möglichen Punkte: D2(-2|-2|6) und D3(10|2|2).
| Downloads |
PowerPoint